Selection of Air Ejectors Part I. Basic design, operating information, and operation limitations of air ejectors. Blatchley Schutte & Koerting An ejector is a pump which uses the jet action of one fluid to entrain and compress another fluid. The high velocity primary stream is produced by expanding a high.
Eductor calculations
Eductor calculations
I am a new engineer and am looking for pointers on calculating the flowrate needed to move a gas.
We have up to a 150# steam supply as the motive stream. The question is what pressure can we regulate this steam to in order to still maintain the flow.
We are passing the steam at some pressure (this is what is to be determined) through the eductor to induce the flow of a stack gas, which is at or near atmospheric pressure (may actually be a slight vacuum). The outlet of the eductor will have a stack gas/steam mixture that will then be returned to the stack. This flow will serve as a 'fast loop' that every so often an analyzer will pull a 'slip stream' from to test.
Any suggestions as to how to formulate a relation of motive stream to outlet pressure? The eductor used for gases is basically a converging/diverging nozzle from what I understand. The pressure of the motive stream is dropped, to increase its velocity. This in turn sucks the stack gas into the eductor. The two then exit the eductor at an intermediate pressure.
Also, any good sites that thoroughly explain steam usage in refineries? I am looking for something that starts with the basics of steam.
Thank you...
- 6 Design of new ejector and comparison with measured ejector We will find the new ejector which has greater mass flow rate in the suction branch (mass flow of air) than the original ejector for pressure 90-100 kPa. This we must find new dimensions of ejector which meets this conditions. Diameter of throat ( Dk) and diffusor ( Dv) are changed.
- The most comprehensive source of design information for ejectors can be found in a series of Engineering Sciences Data Unit (ESDU) data items, Nos. 85032 and 84029. 6 Design of new ejector and comparison with measured ejector We will find the new ejector which has greater mass flow rate in the suction branch (mass flow of air) than the original.
- 2 (L) Schematic of an ejector; (R) Parameters of an ejector in calculation 4. Experimental set up 4.1. Experimental testing device For a purpose of measuring the actual performance of an ejector cycle, an indoor testing device was set up. Figure 3 shows a schematic of the whole set of testing device, which consists of a vapor generator.
The basic SI unit of force is the newton, which has the symbol N.One newton is defined as the force necessary to give a mass of 1 kg an acceleration of 1 m/s2. The acceleration due to gravity is normally taken as 9.81 m/s2. This is the acceleration imparted to a 1 kg force by its own weight (1 kg-force). Hence:
1 kg-force = 9.81 N
1 tonne-force = 9810 N or 9.81 kN
Note: For less precise calculations the value of g is often taken as 10 m/s2. The SI unit of pressure and stress is the pascal, which has the symbol Pa.
1 Pa = 1N/m2
1MPa= 1 MN/m2 or 1 N/mm2
1 GPa = 1 GN/m2 or 1 kN/mm2
Air Ejector Design Calculations
Note: The SI system actually uses the designation 9/81 ms–2 for the acceleration of gravity (g) and a similar system for other units. However, to avoid confusion the traditional
designation is being used here.
Formulae
The following formula may be used for calculating the ejection force:
This is the way the formula is usually written in scientific texts but a slightly easier form for computational purpose is:
where:
Fp = the ejection resistance force (N)
E = Young’s modulus of the polymer (N/cm2)*
A = total surface area of moulding in contact with cavity or core, in line of draw (cm2)*
μ= coefficient of friction, polymer on steel
m = Poisson’s ratio
d = the diameter of a circle whose circumference is equal to the total projected perimeter of the moulding (cm)*
∝= the coefficient of linear expansion of the polymer (cm/°C)*
Δt= (polymer softening temperature) (mould tool temperature) (°C)
t = average wall thickness of part (cm)*
*Note that the units of length here are all in cm.
Example
A two-impression thin walled box-shaped component is to be moulded on a 275 tonne press. The machine has an ejector force rated at 40 kN. Calculate whether this is sufficient given the following data:
Steam Ejector Design Calculation
Material: Polystyrene (PS)
Young’s modulus of elasticity: 300,000 N/cm2
Poisson’s ratio: 0.35
Coefficient of friction (PS on steel): 0.4
Softening temperature of PS: 80 °C
Mould tool temperature: 20 °C
Coefficient of linear expansion (PS): 0.00007 cm/°C
The dimensions of the box are shown in Figure 10.8: all dimensions are in cm.
Total area of resistance = 2 x (12 x 15) + 2 x (12 x 25) = 360 + 600 = 960 cm2
Total projected perimeter = 2 x 15 + 2 x 25 = 80 cm
Hence:
d = 80/π = 25.46 cm and Δt = 80 20 = 60 °C
Therefore,
p F = 13 824 N, or 13.8 kN
Hence for a two-impression tool we require 2 x 13.8 kN = 27.6 kN. This is well within the machine specification of 40 kN; however, in practice the machine ejection force will also be subject to the sliding resistance of the ejector system and sometimes to force
exerted by any return springs used in the ejector assembly.
A good rule of thumb is to apply a factor of 1.25 for nonspring systems and 1.5 for spring return systems. Therefore, in this case the total ejection resistance force is:
1.25 X 27.6 = 34.5 kN for non-spring systems, or
1.5 X 27.6 = 41.4 kN for spring return systems
This demonstrates that the machine ejection force is satisfactory for the first case but unsatisfactory for the second case.
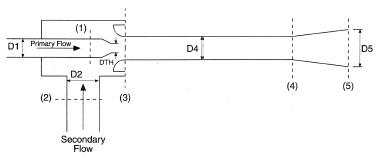
Air Ejector Design
Please contact me if you would like a excel spread sheet for this calculation.